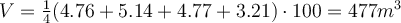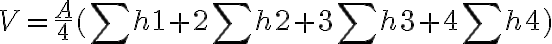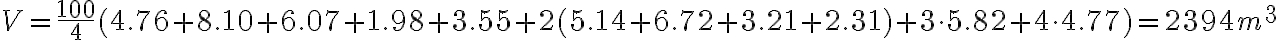Geodézia építészeknek jegyzet - Log in
9. Földtömegszámítás
9.1. Földtömegszámítás rácsháló alkalmazásával
Ezt a módszert például munkagödrök térfogatának kiszámításához célszerű alkalmazni, amikor az eredeti terep változása egyenletes és a munkagödör feneke vízszintes, esetleg lépcsős kialakítású. A földmunka területén egy négyzet, esetleg háromszög vagy téglalap alapú rácshálót kell kialakítani, és a háló pontjaiban ki kell számolni a munkagödör mélységét (az eredeti terep és a munkagödör fenekének magasságkülönbségét). Minél sűrűbben vesszük fel a rácspontokat, annál pontosabb eredményt kapunk, ugyanakkor a számítás mennyisége is jelentősen megnőhet. Célszerű valamilyen ésszerű középutat választani.
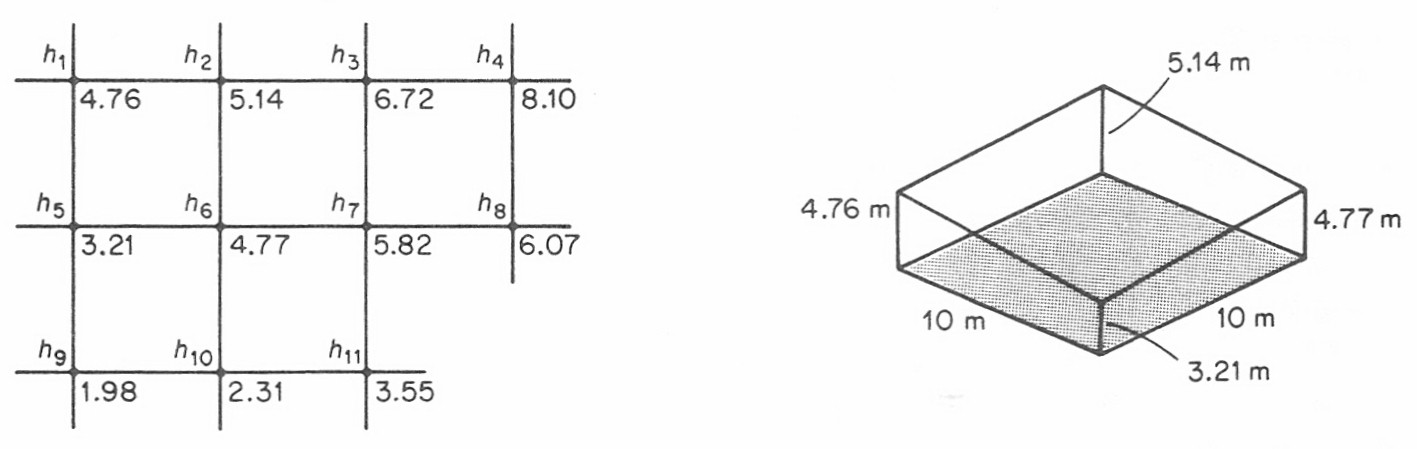
Feltételezzük, hogy a rácspontok között a munkagödör mélysége lineárisan változik, így a háló egy mezőjére vonatkozóan a térfogat az alapterület és az átlagos mélység szorzataként számítható, a fenti ábra alapján:
Hasonló számítás végezhető minden mezőre, négyzetháló esetén a következő általános képletet kapjuk:
ahol
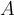 a négyzetháló egy rácsmezőjének területe
a négyzetháló egy rácsmezőjének területe
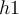 a
rácsháló azon mélységei, amelyeket csak egyszer használunk a számítások során, pl.
a
rácsháló azon mélységei, amelyeket csak egyszer használunk a számítások során, pl. 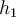
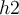 a
rácsháló azon mélységei, amelyeket kétszer használunk a számítások során, pl.
a
rácsháló azon mélységei, amelyeket kétszer használunk a számítások során, pl. 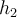
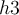 a
rácsháló azon mélységei, amelyeket háromszor használunk a számítások során, pl.
a
rácsháló azon mélységei, amelyeket háromszor használunk a számítások során, pl. 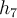
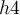 a
rácsháló azon mélységei, amelyeket négyszer használunk a számítások során, pl.
a
rácsháló azon mélységei, amelyeket négyszer használunk a számítások során, pl. 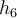
Nem négyzet alapú háló esetén az egyes mezőkre vonatkozó térfogatokat külön-külön kiszámítjuk, majd összegezzük. A fenti példa szerint:
A fenti
számpéldát [Uren és Price, 1985]-ből
vettük.